Mathematical Analysis and Generation of Farey Fractals

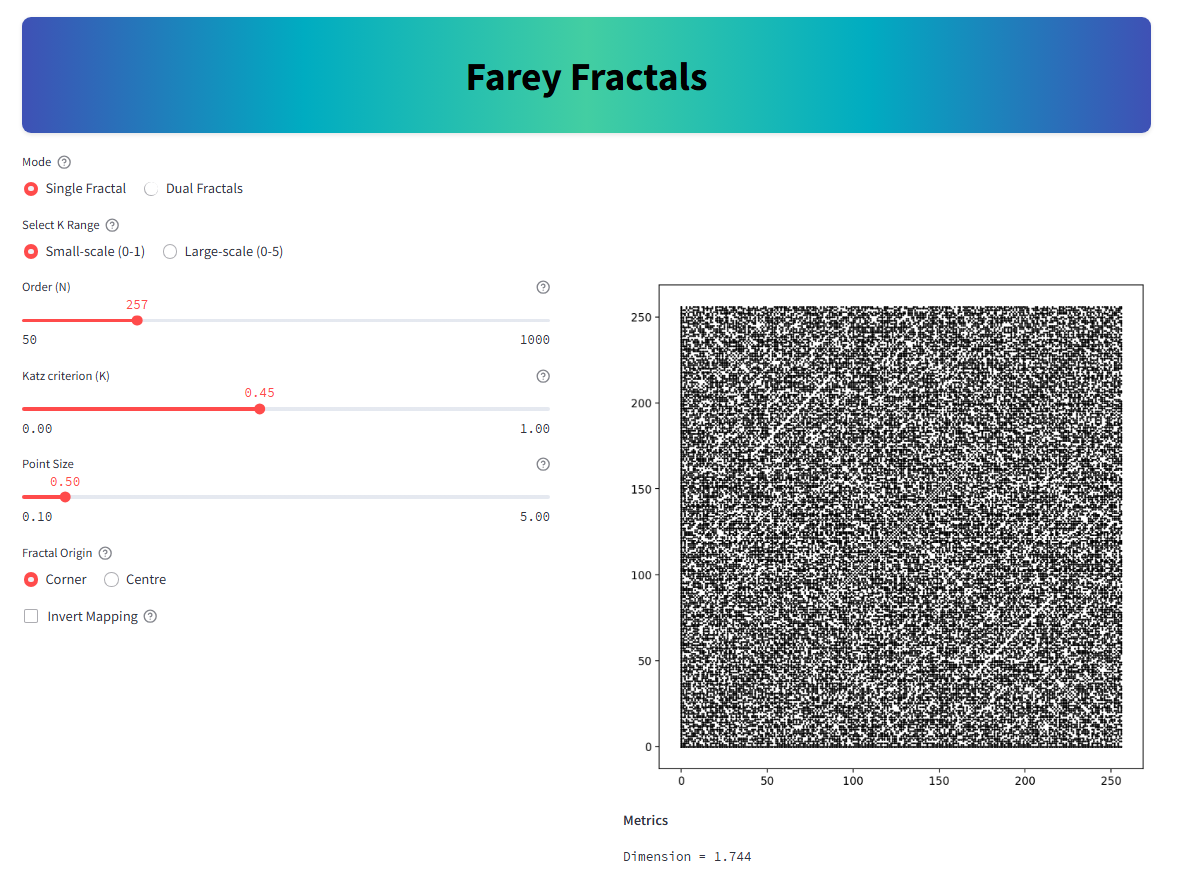
This thesis presents a comprehensive study of Farey fractals - intricate, self-similar geometric structures derived from the Farey sequence of rational numbers. The research bridges number theory, geometry, and computational analysis to uncover how simple arithmetic relationships can generate fractal complexity.

The project develops algorithms to construct Farey fractals under varying parameters and investigates their qualitative and quantitative characteristics. Visual analyses reveal distinct structural symmetries and transformations, while quantitative methods such as box-counting fractal dimension and Hausdorff distance provide formal measures of scaling complexity and geometric continuity.

By simulating Farey fractals across parameter ranges and comparing them through both visual and metric perspectives, the study highlights the fractals' sensitivity to parameter variation and their convergence properties. These findings contribute to a broader understanding of how mathematical sequences can encode fractal geometry, offering insights that may extend to imaging methodologies, signal analysis, and mathematical modelling.

To access the dashboard, visit https://daniel-cottrell-farey-fractals.streamlit.app/